Rat in a Maze puzzle | Backtracking

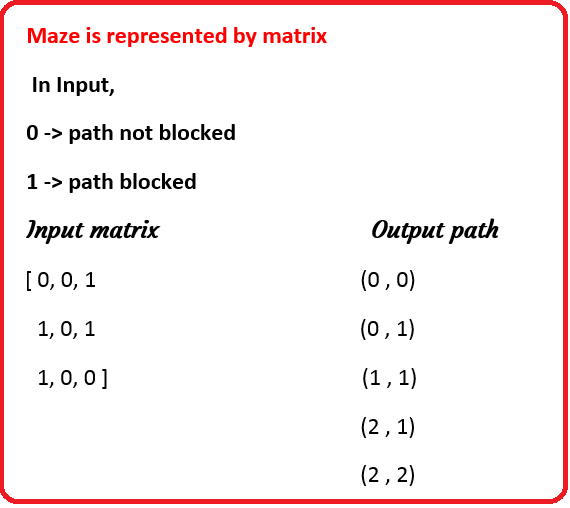
Question:

Write a program to solve the rat in a maze puzzle. Given a maze, NxN matrix. A rat has to find a path from source to destination. maze[0][0] (left top corner)is the source and maze[N-1][N-1](right bottom corner) is destination. There are few cells which are blocked, means rat cannot enter into those cells.

Approach:

Firstly, we will make a matrix to represent the maze, and the elements of the matrix will be either 0 or 1. 1 will represent the blocked cell and 0 will represent the cells in which we can move. While moving through the maze we mark the current position as 1 in result matrix. Finally, after the destination is reached then we print the index with 1 in result matrix. This is the path.

Algorithm:

Check for the current cell, if it is the destination cell, then the puzzle is solved.
If not, then we will try to move right and see if we can move in the right cell or not (to move in a cell it must be vacant and not already present in the path).
If we can move there, then we will continue with the path taken to the next right cell.
If not, we will try to move to the downward cell. And if it is blocked or taken, we will move left.
Similarly, if we can’t move left as well, we will simply move to the upward cell.
If none of the four moves ( right, down, left, up) are possible, we will simply move back and change our current path (backtracking).

NOTE:

It is important to check the previous direction in which the rat has moved because if rat will move in the opposite direction w.r.t its previous direction then rat might end up in infinite loop. Example: if rat has moved to its left in the previous direction then if in next moves to right then moving left option will be available again then rat will move to left again , then again right and so on.

Program

import java.util.Scanner;
class RatMaze
{
  static int r,c;                               //class (or) global scope 
  public static void main(String ar[])
  {
    int i,j;
    
    Scanner sc = new Scanner(System.in);
    System.out.println("Enter number of rows");
     r = sc.nextInt();
    System.out.println("Enter number of columns");
    c = sc.nextInt();
    int matrix[][] = new int[r];
    System.out.println("Enter matrix elements..\n 0->path not blocked \n 1->path blocked");
    for( i=0; i<r; i++)
      for( j=0; j<c ;j++)
         matrix[i][j] = sc.nextInt();
    
    System.out.println("Enter Starting row and column");
    int r1 = sc.nextInt();
    int c1 = sc.nextInt();
    
    
    System.out.println("Enter ending row and column");
    int r2 = sc.nextInt();
    int c2 = sc.nextInt();
    
    int result[][] = new int[r];
    
    int status = findPath(matrix, result, r1, c1,'N', 'N', r2, c2);
    if( status< 0)
      System.out.println("Rat cannot find cheese in the maze status: "+ status);
    else 
      System.out.println("Successful status: "+ status);
     
  }
  static int findPath(int matrix[][], int result[][], int curR,int curC, char previous,char direction, int destR,int destC)
  {
    int status = -1;                                            //Used to check whether destination reached or not
     
    if(curR<r && curC<c)
    {
      int i,j;
      
      if(matrix[curR][curC] == 1)
           return -1;                                           // Path Blocked
      if(matrix[curR][curC] == 0)
      {
        if(curR == destR && curC == destC)
        {
          result[curR][curC] = 1;
          for( i=0; i<r; i++)
            for( j=0; j<c ;j++)
          {
            if(result[i][j] == 1)
              System.out.println("("+i +" , " +j +" )");
          }
          return 1;                                              //return status 'success'
       
        }
        /*If status is -1(destination not reached yet) and it is not deadlock condition,
         * then Recursive calls are made to find the path*/ 
        
        if(previous != 'L' && status != 1)                      //previous direction not Left
        {
          result[curR][curC] = 1;                               //updating the path of result matrix
          System.out.println("Turning Right");
          status = findPath(matrix, result, curR, curC+1, direction, 'R', destR, destC);
        }
        if(previous != 'U' && status != 1)                      //previous direction not Up
        {
          result[curR][curC] = 1;
          System.out.println("Turning Bottom");
          status = findPath(matrix, result, curR+1,curC ,direction,'B', destR, destC);
        }
        if(previous != 'R' && status != 1)                       //previous direction not Right
        {
          result[curR][curC] = 1;
          System.out.println("Turning Left");
          status = findPath(matrix, result, curR,curC-1 ,direction,'L', destR, destC);
        }
        if(previous != 'B' && status != 1)                        //previous direction not Bottom
        {
          result[curR][curC] = 1;
          System.out.println("Turning Top");
          status = findPath(matrix, result, curR-1,curC ,direction,'T', destR, destC);
        }
        
      }
    }
    return status;
  }
}

References:

Backtracking TutorialHorizon Rat in a Maze

Codesdope Backtracking to solve rat in a maze