Sort the Matrix Diagonally

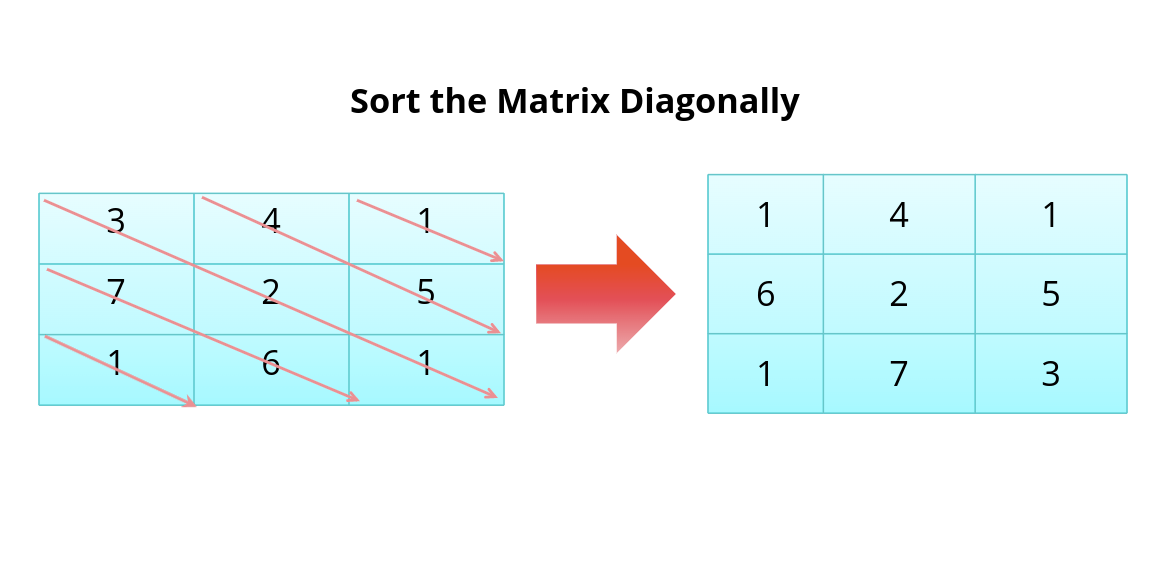
Given a matrix, sort the matrix diagonally. A matrix diagonal is a diagonal line of cells starting from some cell in either the topmost row or leftmost column and going in the bottom-right direction until reaching the matrix’s end. For example, the matrix diagonal starting from mat[2][0], where mat is a 6 x 3 matrix, includes cells mat[2][0], mat[3][1], and mat[4][2].

Given an m x n matrix mat of integers, sort each matrix diagonal in ascending order and return the resulting matrix.

Example 1:

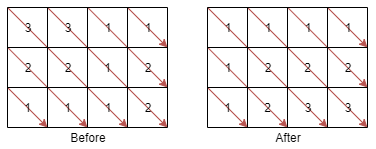
Input: mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]
Output: [[1,1,1,1],[1,2,2,2],[1,2,3,3]]

Example 2:

Input: mat = [[11,25,66,1,69,7],[23,55,17,45,15,52],[75,31,36,44,58,8],[22,27,33,25,68,4],[84,28,14,11,5,50]]
Output: [[5,17,4,1,52,7],[11,11,25,45,8,69],[14,23,25,44,58,15],[22,27,31,36,50,66],[84,28,75,33,55,68]]

 Sort Matrix Approach:

1. We have to sort the matrix diagonally. For that find the starting point for all the diagonals.
2. All the first row cells([0][0], [0][1], [0][2] ) and first column cells ([0][0], [1][0], [2][0] ) are the starting point of diagonals.
3. You can see that the first row cells have the same row index and the first column cells have the same column index.
4. After finding a starting point for a diagonal, use bubble sort  to sort the elements in that diagonal.

Program:

class Solution {
    public int[][] diagonalSort(int[][] mat) 
    {
        //rowwise start
        //x axis increase y axis decrease from starting point
        
        int row = mat.length;
        if(row==0)
            return mat;
        int col = mat[0].length;
        
        //find all starting point in first column
        for(int k = 0; k<row; k++)
        {
            int x = k;
            int y = 0;   //column index fixed
            int ele = mat[x][0];
            bubblesort(mat, x,y,row,col);
        }
        
        
        //find all the starting points in first row
        for(int l = 1; l<col; l++)
        {
            int y = l;
            int x = 0;   // row index fixed
            bubblesort(mat,x,y,row,col);
        }
        return mat;
    }
    
    void bubblesort(int[][] mat, int x,int y, int row, int col)
    {
        
        for(int r1=x, c1=y;     r1<row && c1<col;    r1++,c1++)
        {
            for(int r2=r1+1, c2=c1+1;   r2<row && c2<col;    r2++,c2++)
            {
                ///move smallest element to front
                if(mat[r1][c1] > mat[r2][c2])
                {
                    int temp = mat[r1][c1];
                    mat[r1][c1] = mat[r2][c2];
                    mat[r2][c2] = temp;
                }
            }
        }
    }
    
}

You Might also like..

Exit Point in a Matrix | Samsung

Upper or lower triangular matrix