Min Cost Climbing Stairs | Dynamic Programming

You are given an integer array cost where cost[i] is the cost of i^th step on a staircase. Once you pay the cost, you can either climb one or two steps.

You can either start from the step with index 0, or the step with index 1.

Return the minimum cost to reach the top of the floor.

Example 1:

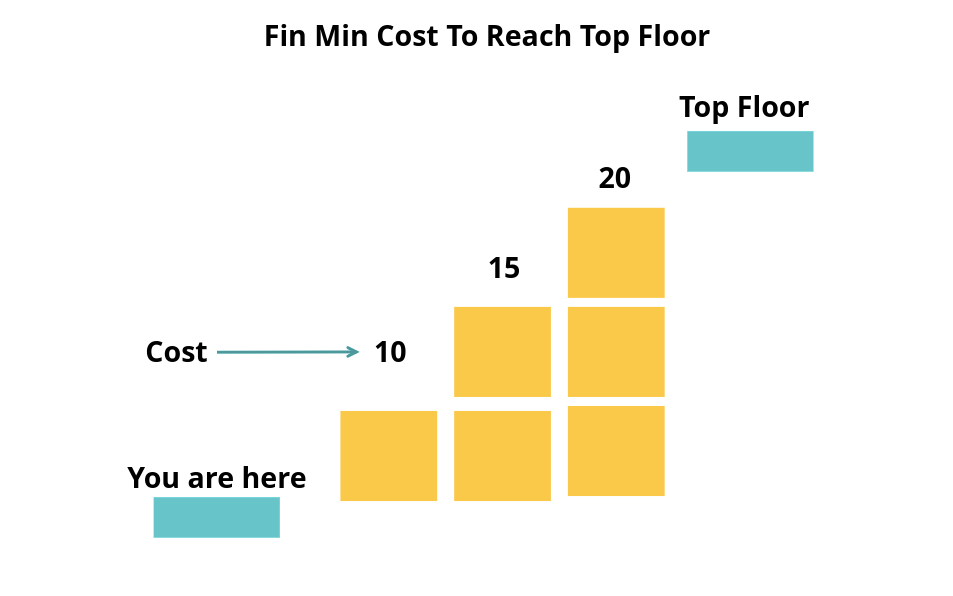
Input: cost = [10,15,20]
Output: 15
Explanation: You will start at index 1.
- Pay 15 and climb two steps to reach the top.
The total cost is 15.
Imagine the stairs like this: 
                    __TopFloor
                  20  
                15 
              10
You are here__

Example 2:

Input: cost = [1,100,1,1,1,100,1,1,100,1]
Output: 6
Explanation: You will start at index 0.
- Pay 1 and climb two steps to reach index 2.
- Pay 1 and climb two steps to reach index 4.
- Pay 1 and climb two steps to reach index 6.
- Pay 1 and climb one step to reach index 7.
- Pay 1 and climb two steps to reach index 9.
- Pay 1 and climb one step to reach the top.
The total cost is 6.

Approach 1:

We can solve this using Dynamic Programming. In DP we have two different approaches, the top-down and bottom-up. First, let’s solve using a bottom-up approach. In the bottom-up approach, small subproblems are computed first after that solution for the original problem is computed. At each step, we have take minimum of previous two step cost and add that to current step cost. We can reach top floor either from n-1th step or n-2th step. So,
Result = Minimum of ( cost to reach n-1 , cost to reach n-2 )

Base case: 
For the first two steps, minimum cost to reach the step is same as cost.
For example, cost = [10,15,20]
mincost(0) = cost[0] = 10
mincost(1) = cost[1] = 15

 Program:

public int minCostClimbingStairs(int[] cost) 
{
    int n = cost.length;
    if(n == 0)
        return 0;
    else if(n == 1)
        return cost[1];
    else if(n==2)
        return Math.min(cost[0],cost[1]);
    //Base cases
    int[] mem = new int[n];
    mem[0] = cost[0];
    mem[1] = cost[1]; 

    //Now to reach next step, 
    //we have take minimum of previous two steps and add that to current step cost
    for(int i = 2; i<n; i++)
    {
        mem[i] = Math.min(mem[i-1],mem[i-2]) + cost[i];
    }
    return Math.min(mem[n-1],mem[n-2]);
}

Approach 2:

In the top-down approach, we start with the original problem and break it into smaller chunks. We can reach the top floor ‘n’ step either from n-1th step or n-2th step. So we solve for n-1 and n-2 and combine their result to compute min cost for climbing nth step. Remember each subproblems result as mem array.

Recurrence Relation:
mincost(i) = cost[i]+min(mincost(i-1), mincost(i-2))

Program:

public int minCostClimbingStairs(int[] cost) 
{
    int n = cost.length;

    //Store intermediary results in mem array
    int[] mem = new int[n]; 
    return Math.min(find(n-1,cost,mem), find(n-2,cost,mem));

}
int find(int n, int cost[],int mem[])
{
    if(n< 0)
        return 0;

    if(mem[n] != 0)
        return mem[n];

    mem[n]  = cost[n] + Math.min(find(n-1,cost,mem),find(n-2,cost,mem));
    return mem[n];
}

You Might Also Like:

Climbing Stairs Interview Question

House Robber Interview Question