Find Min Path Sum In Triangle
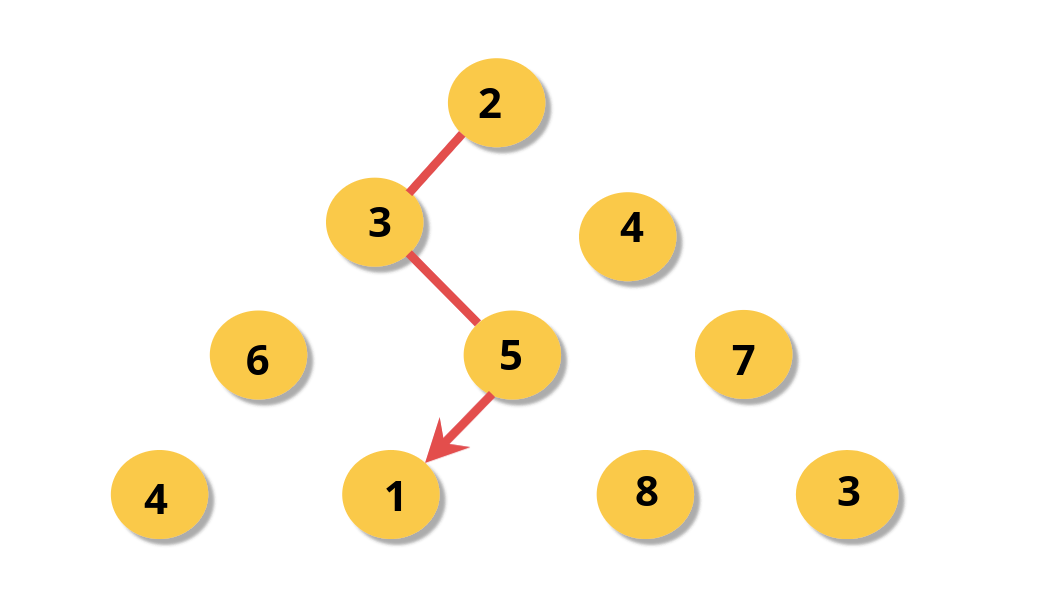
Given a triangle array, find min path sum in triangle. Find the shortest path/ path with a minimum sum in the triangle from top to bottom.
For each step, you may move to an adjacent number of the row below. If you are on index i on the current row, you may move to either index i or index i + 1 on the next row.
Example 1:
Input: triangle = [[2],[3,4],[6,5,7],[4,1,8,3]] Output: 11 Explanation: The triangle looks like: 2 3 4 6 5 7 4 1 8 3 The minimum path sum from top to bottom is 2 + 3 + 5 + 1 = 11 (underlined above).
Example 2:
Input: triangle = [[-10]] Output: -10
Approach 1:
Imagine it like a binary tree. We can use a top-down approach. To solve for the root, we must know the minimum path sum of its children.
Let’s take an example,
6
4 1
From the root, we can take either of the two paths whichever is minimum. We know that 4 and 1 are leaf nodes. Min path of leaf nodes will be equal to its node value.
MinPath(6) = 6 + Minimum of (MinPath(4), MinPath(1)) MinPath(6) = 6 + Minimum of ( 4, 1) MinPath(6) = 6 + 1 = 7
Recurrence Relation:
Min Path sum = root.value + Math.min( minPath(root.left), minPath(root.right) )
Base cases:
All the leaf nodes will have their value as minPath.
Program:
class Solution {
public int minimumTotal(List<List<Integer>> triangle)
{
if(triangle.isEmpty())
return 0;
int current = triangle.get(0).get(0);
int i = 0, currentLevel = 0;
return current + Math.min(recur(i,currentLevel+1,triangle), recur(i+1, currentLevel+1,triangle ));
}
int recur(int i,int level, List<List<Integer>> triangle)
{
if(triangle.size() == level)
{
return 0;
}
int current = triangle.get(level).get(i);
return current + Math.min(recur(i,level+1,triangle) , recur(i+1, level+1, triangle));
}
}
Analysis:
Time Complexity – O(2^n) where n is the no. of elements in a triangle. We have exponential time complexity because in each node we can take two paths.
Space Complexity – O(1) since we are not using any extra space
Approach 2:
In the above approach, the path sum is calculated twice for node 5. One for parent 3 and one for parent 4.
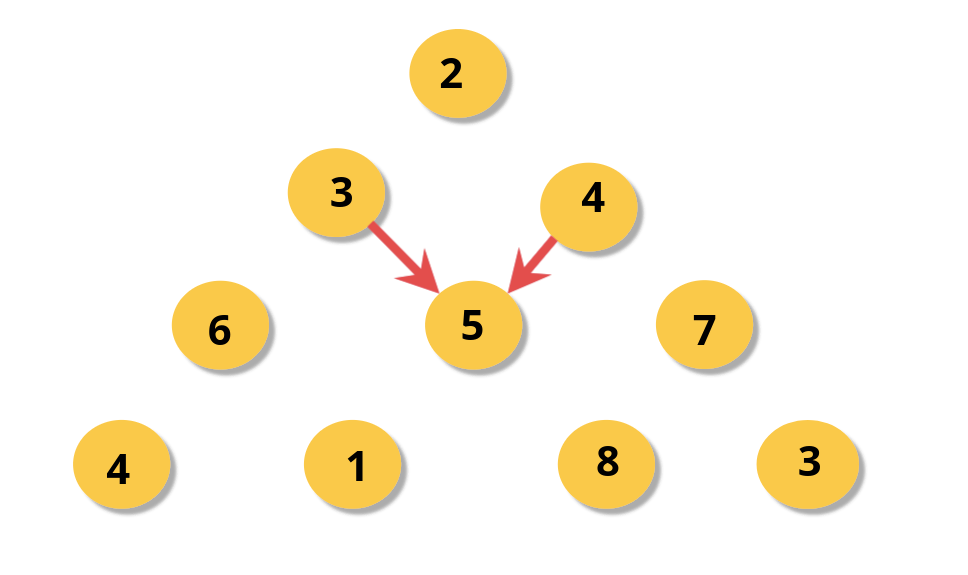
We can optimize it using a jagged array. We can store the computed min path sum of each node in a jagged array. The jagged array will be of the same size as the input array.
Program:
class Solution {
public int minimumTotal(List<List<Integer>> triangle)
{
if(triangle.isEmpty())
return 0;
int[][] computed = new int[triangle.size()][];
//Creating jagged array to store computed value
for(int i =0; i<triangle.size(); i++)
{
int innersize = triangle.get(i).size();
computed[i] = new int[innersize];
for(int j =0; j<innersize; j++)
{
computed[i][j] = -1;
}
}
int current = triangle.get(0).get(0);
int i = 0, currentLevel = 0;
return current + Math.min(recur(i , currentLevel + 1,triangle,computed), recur(i+1, currentLevel + 1,triangle,computed ));
}
int recur(int i,int level, List<List<Integer>> triangle, int[][] computed)
{
if(triangle.size() == level) //reached leaf
{
return 0;
}
//precomputed value is returned if the node is already visited
int computedValue = computed[level][i];
if(computedValue != -1)
{
return computedValue;
}
int current = triangle.get(level).get(i);
int minPathSum = current + Math.min(recur(i,level+1,triangle,computed) , recur(i+1, level+1, triangle,computed));
computed[level][i] = minPathSum;
return minPathSum;
}
}
Analysis:
Time Complexity – O(n) Since we visit each element in the array once.
Space Complexity – O(n) Since we store the computed path sums in an extra array. The size of the extra array is equal to the size of the input array.
You Might Also Like…
Min Cost Climbing Stairs | Dynamic Programming

