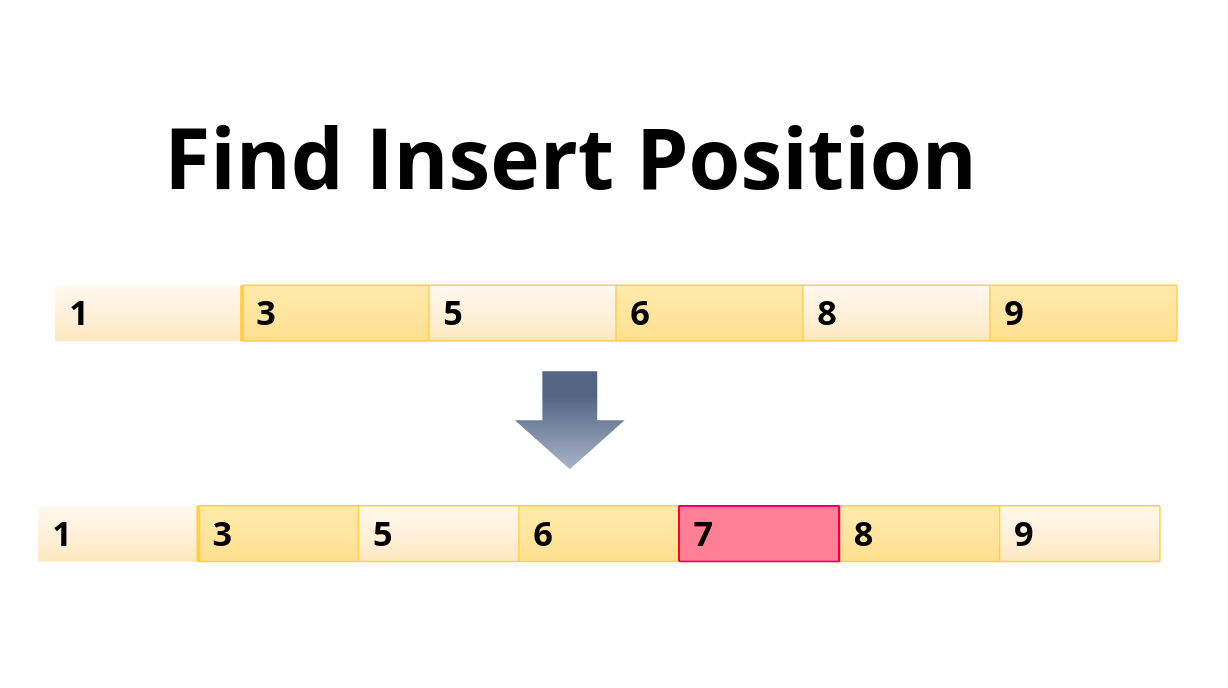
Find the Insert Position in Sorted Array
Question
Given a sorted array of distinct integers and a target value, return the index if the target is found. If not, return the index where it would be if it were inserted in order.
You must write an algorithm with O(log n) runtime complexity.
Example 1:
Input: nums = [1,3,5,6], target = 2
Output: 1
Explanation: Insert Position for 2 is 1. Index starts from 0. After insert array will look like this [1,2,3,5,6]
Example 2:
Input: nums = [1,3,5,6], target = 5
Output: 2
Explanation: 5 will be inserted after 3.
Example 3:
Input: nums = [1,3,5,6], target = 7
Output: 4
Explanation: 7 will be inserted as the last element after 6.
Linear Search Approach
Since the array is sorted, we can search through the array one by one. When array element >= target then insert position is the current index position.
Solution()
{
int i;
for( i=0; i < nums.length; i++)
{
if(nums[i] >= target)
{ return i;
}
}
}
Time complexity: O(n) because we traverse whole array to find the insert position.
This is fairly simple but above approach is not accepted because in the question it is mentioned that we must solve in O(logN).
First thing that comes to our mind when see sorted array and O(logN) is Binary Search.
Binary Search Approach
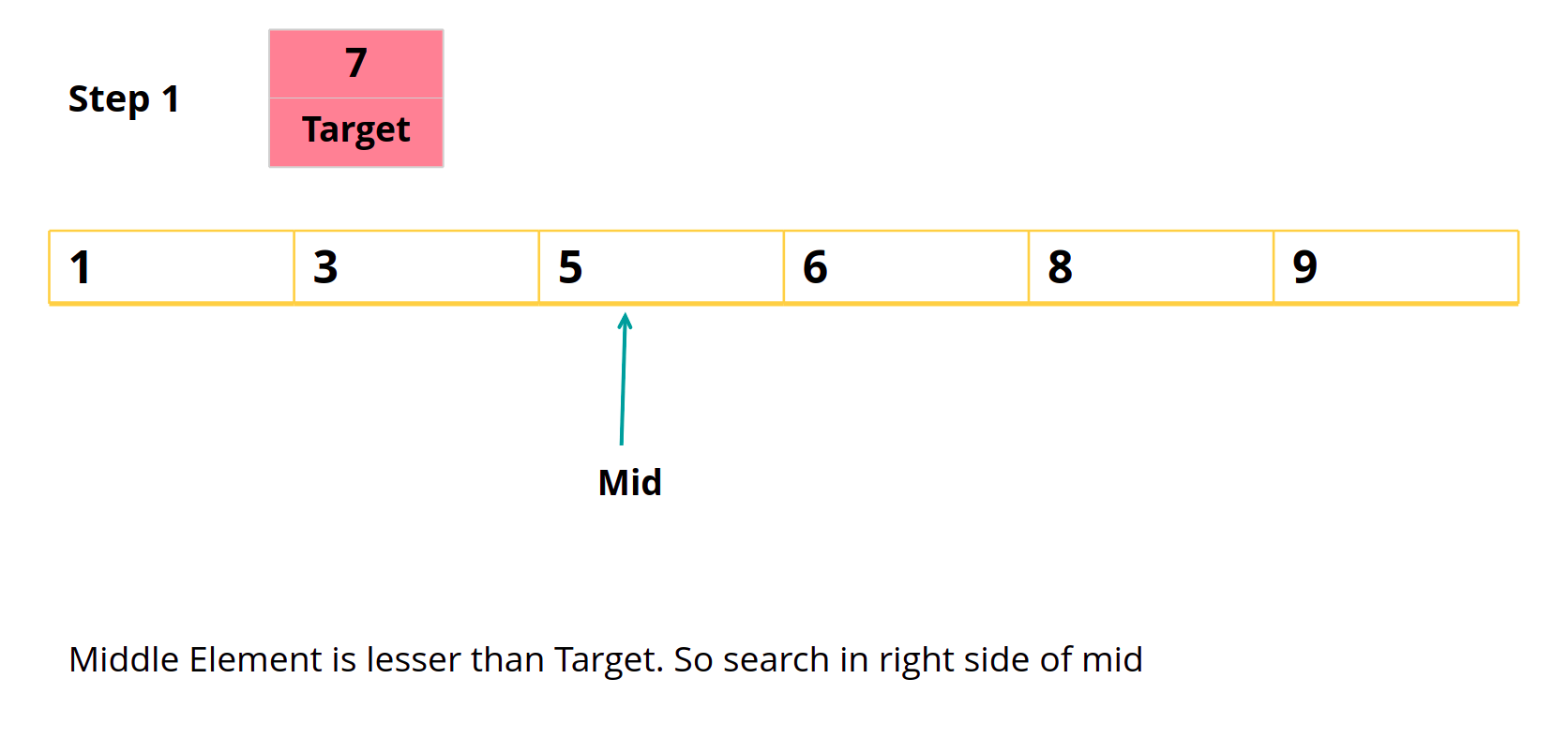
We use Binary Search to find the insert position. Usually in binary search we find a particular element, but here we want to find the insert position. Consider the below cases before writing code.
case 1: Target Element is lesser than first element of array
case 2: Target Element is greater than last element of array
case 3: Target Element need to be inserted somewhere inside the array
During Binary Search if we reach start or end of the array( case 1 and case 2) and target is not found, then insert position is 0 or n-1 respectively.
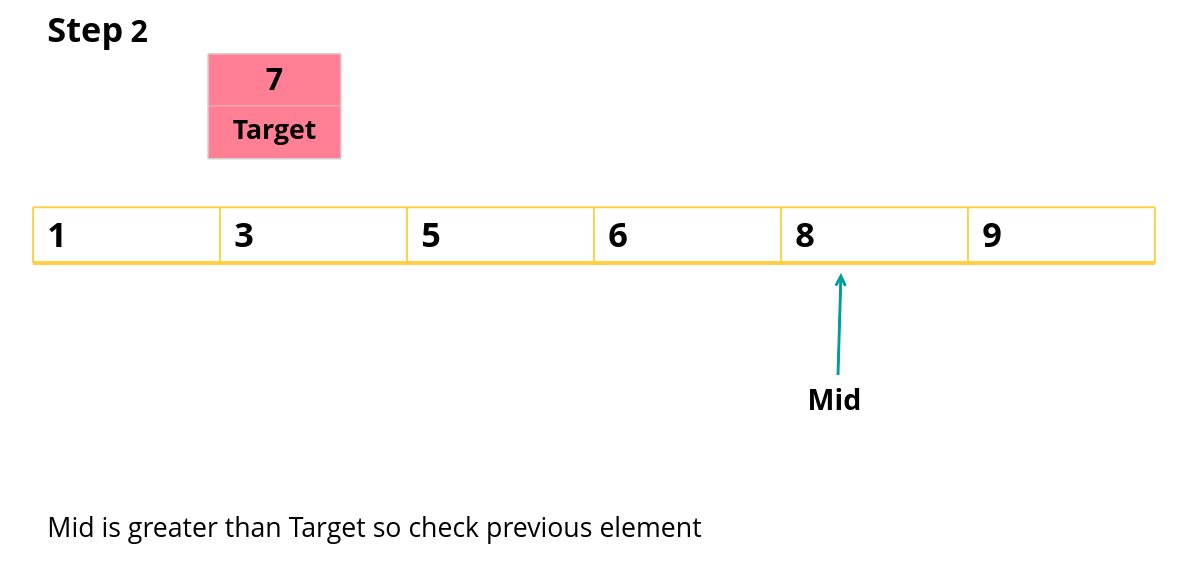
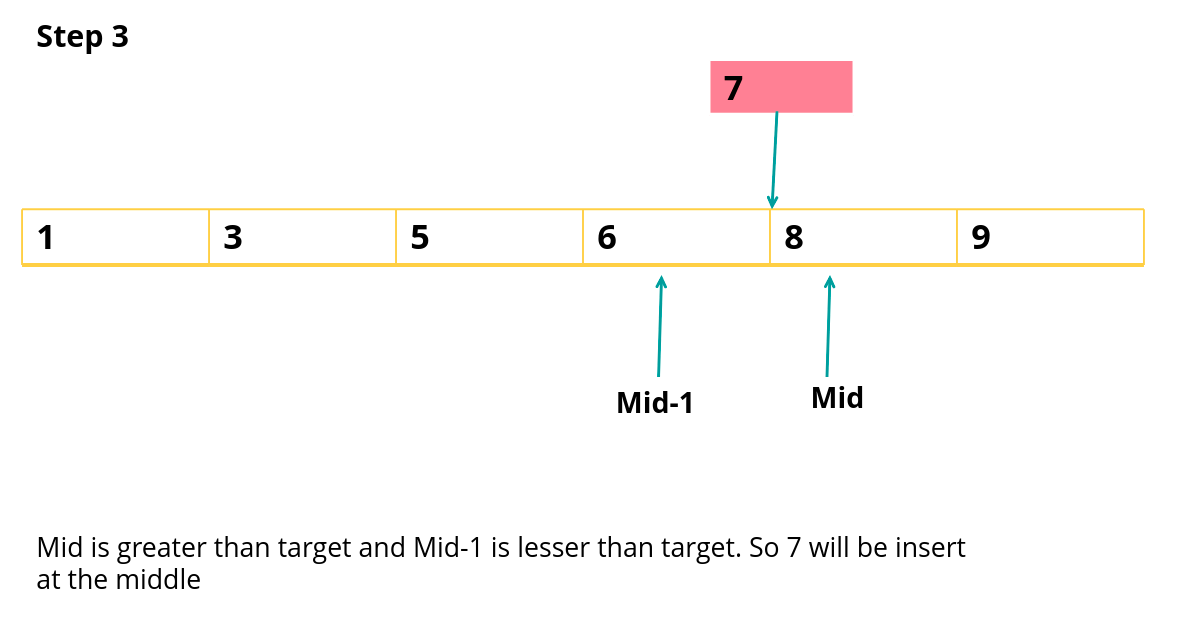
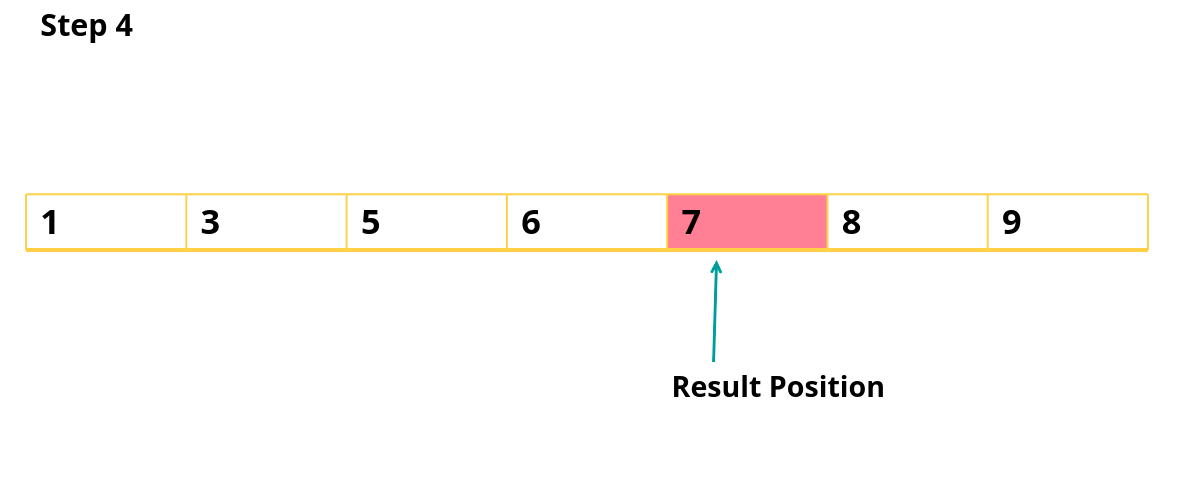
Consider the following example,
Array: [1,3,5,6,7,8,9]
Target: 7
Program
class Solution
{
public int searchInsert(int[] nums, int target)
{
int low = 0;
int high = nums.length-1;
int n = nums.length;
while(low<=high)
{
int middle = (low+high)/2;
if(nums[middle] > target )
{
// when target is smaller than starting element of array
// previous element is smaller and current element is larger than target
if (middle == 0 || nums[middle-1] < target)
{
return middle;
}
high = middle-1;
}
else if(nums[middle] < target)
{
// target is larger than last element
if(middle == n-1)
{
return middle+1;
}
low = middle+1;
}
else
{
return middle;
}
}
return -1;
}
}

