Minimum count of numbers in the Fibonacci number
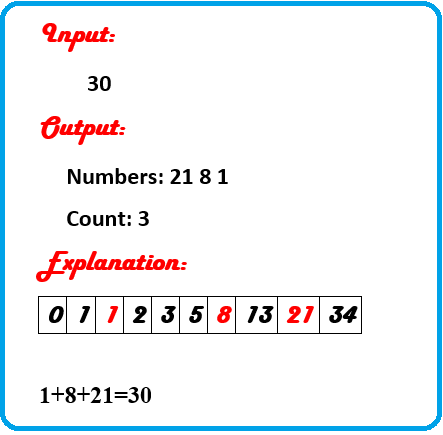
Question:
To find the minimum count of numbers in the Fibonacci series and their sum is equal to the number n.
Fibonacci Series
F (0) = 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 …
In some texts, it is customary to use n = 1. In that case, the first two terms are defined as 1 and 1 by default, and therefore:
F (1) = 1, 1, 2, 3, 5, 8, 13, 21, 34 …
Logic:
- Generate the Fibonacci series to find the count.
- Pass the series and n to the function.
- Find the nearest smaller Fibonacci no to n and increment the count.
- Then subtract the nearest number with n and assign value to n.
- And Recursively repeat the process until n becomes zero.
Program:
#include<stdio.h>
int sum(int a[],int n)
{
static int c=0; //minimum no of count to reach the number n
int i;
for(i=0;i<30;i++)
{
if(a[i]>n)
{
printf("%d ",a[i-1]);
n=n-a[i-1]; //a[i-1] is the nearest smaller number to n
c++; //increment the count
break;
}
}
if(n==0) //return the count when number is zero
return c;
else
sum(a,n); //call the function recursively
}
void main()
{
int a[100],i,count=0,n;
printf("Enter the number:");
scanf("%d",&n);
a[0]=0,a[1]=1;
for(i=2;i<30;i++) //generates the Fibonacci series
{
a[i]=a[i-1]+a[i-2];
}
count=sum(a,n); //Pass the value and array to find the minimum count
printf("Count: %d",count);
}

